Función Exponencial

octubre 02, 2017

Función Exponencial

Consideremos un número real fijo $a> 0$ , con $a\neq 1$ . La función exponencial de base a es una función de la forma $f(x)=a^{x}$ .
En una función exponencial, lo que varía aquí es el exponente x, no la base a.

Propiedades de la Función Exponencial

$f(0)=1$
Por ejemplo, si $f(x)=3^{x}$ , entonces $f\left ( 0 \right )= 3^{0}$ . Como todo número elevado a la cero es igual a 1, entonces vemos que sí se cumple la propiedad.
$f\left ( x \right )>0$ para todo x.
Es decir las imágenes de la función siempre serán números positivos, sin importar el valor de la x.
$f\left ( x_{1}-x_{2} \right )=f\left ( x_{1} \right )\cdot f\left ( x_{2} \right )$
Por ejemplo, tomando la función $f\left ( x \right )=3^{x}$ , vemos que $f(1+2)=f(3)=3^{3}=27$
Y por otro lado, $f(1)\cdot f(2)=3^{1}\cdot 3^{2}=3\cdot 9=27$
Pudimos verificar que $f\left ( 1+2 \right )=f\left ( 1 \right ) \cdot f\left ( 2 \right )$ . En este ejemplo $x_{1}=1$ y $x_{2}=2$ .
$f\left ( x_{1}-x_{2} \right )=\frac{f\left ( x_{1} \right )}{f\left ( x_{2} \right )}$
Por ejemplo, tomando la función $f\left ( x \right )=3^{x}$ , vemos que $f(3-2)=f(1)=3^1=3$
Y por otro lado,
$\frac{f(3)}{f(2)}=\frac{3^3}{3^2}=\frac{27}{9}=3$
Pudimos verificar que $f\left ( 3-2 \right )=\frac{f\left ( 3 \right )}{f\left ( 2 \right )}$ .
En este ejemplo, $x_{1}=3$ y $x_{2}=2$ .
La función exponencial es inyectiva (o uno a uno).

Ahora te vamos a mostrar algunas gráficas para que veas como se comportan estas funciones y además puedas verificar algunas de sus propiedades, como, por ejemplo la 1, la 2 y la 5.

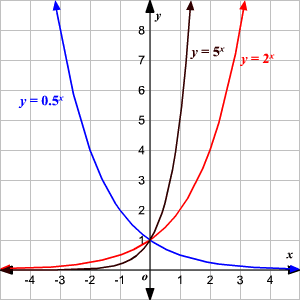
La de arriba es la función $f\left ( x \right )=2^{x}$ . Puedes ver que su gráfica pasa por el punto $\left ( 0, 1 \right )$ , es decir, $f(0)=1$ (propiedad 1). Su gráfica siempre está por encima del eje $X$ , es decir, $f\left ( x \right )> 0$ (propiedad 2).
Dependiendo del valor de la base, así mismo va a ser la forma de la gráfica. Por ejemplo, mira:

Problemas Funciones Exponenciales

El número de habitanctes de Bogotá se triplica cada 40 años. En el tiempo t = 0 , esta población es de 10.000.000 habitantes.

Escribir una expresion (fórmula de la función) para el número de habitantes de Bogotá con respecto al tiempo t.
¿Cuál será la población de la ciudad de Bogotá al cabo de 120 años?

Solución:
Cuando nos hablan sobre algo que se duplica, o se triplica, etc a medida ue pasa cierta cantidad de tiempo, estamos en presencia de un ejercicio de funciones exponenciales.
Para el primer punto de este ejercicio tengamos en cuenta que nos hablan de triplicación. Esto nos dice que la base de nuestra función exponencial es 3.
Además nos dicen que hay una cantidad inical. Esto quiere decir que vamos a anteponer este valor a la potencia de nuestra función. Entonces nuestra expresión para la cantidad de habitantes de Bogotá en función del tiempo es $P\left ( t \right )=10.000.000\cdot 3^{\frac{t}{40}}$
Te preguntarás porqué la presencia de exponente $\frac{t}{40}$ en esta expresión. Esto se debe a que la triplicación ocurre cada 40 años. Mira que cuando t vale 40, esta fracción es igual a 1, y ocurre la primera triplicación; cuando t vale 80, la fracción es igual a 2, y ocurre la segunda triplicación, y así sucesivamente.
Aquí estamos usando la t porque es más usual cuando se nos habla de tiempo.
Para responder la segunda pregunta, basta sólo con cambiar la t por 120.
Entonces tenemos
$P\left ( t \right )=10.000.000\cdot 3^{\frac{120}{40}}\\ =10.000.000 \cdot 3^{3}\\ =10.000.000 \cdot 27 \\=90.000.000$
La respuesta es: al cabo de 120 años, la población será de 270.000.000 de habitantes.