Permutaciones
Primero quiero que leas con atención el siguiente ejemplo. Supón que tienes tres sillas de colores: amarillo, rojo y verde; y las ubicas de todas las maneras diferentes que puedas. Seguramente tendrás algo como esto.
Entonces
Una permutación es cada una de las diferentes maneras en que se puede ordenar un conjunto de elementos.
Hay que decir que aunque sigan siendo los mismos tres elementos, lo que hace que sean diferentes son el orden que tienen en ada arreglo.En el caso del ejemplo anterior, entraron en juego todos los tres elementos, es decir, de las tres tres sillas, hicimos ordenaciones con las tres sillas.
En ese caso, si n representa el número de elementos que vamos a ordenar, la fórmula para saber cuántas ordenaciones diferentes podemos obtener es
En una publicación anterior ya te hablé sobre el factorial. Puedes mirarla otra vez aquí
Es fácil ver que esto se cumple en nuestro ejemplo. Mira: la 
vale 3 porque hay tres sillas. Luego
=3!=6 "P(3)=3!=6")
Ahora veamos un caso un poco más difícil: Supón que agregas una nueva silla. Esta vez, de color negro y quieres saber cuántas diferentes ordenaciones salen, pero solo tomando dos de las cuatro. Vas a obtener algo parecido a esto.
Ahora veamos un caso un poco más difícil: Supón que agregas una nueva silla. Esta vez, de color negro y quieres saber cuántas diferentes ordenaciones salen, pero solo tomando dos de las cuatro. Vas a obtener algo parecido a esto.
Este ejemplo se diferencia del primero en que no todos los elementos del conjunto entraron en juego. Solo una parte fue tenida en cuenta para formar cada permutación.
Si designamos con el número de elementos totales del conjunto y con 
la cantidad de elementos que van a ser tenidos en cuenta, entonces la cantidad de permutaciones, la cual se escribe 
, que se obtiene es
!} "nPk=\frac{n!}{(n-k)!}")
En el caso de nuestro ejemplo, es igual a 4 y igual a 2, y solo tenemos que remplazar las letras por estos números, obteniendo
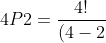!}=\frac{4!}{2!}=\frac{24}{2}=12 "4P2=\frac{4!}{(4-2)!}=\frac{4!}{2!}=\frac{24}{2}=12")
¡Qué tal si pruebas tus habilidades con estos ejercicios!
En el caso de nuestro ejemplo,
¡Qué tal si pruebas tus habilidades con estos ejercicios!
- 10 estudiantes están realizando un examen en el cual los tres con las calificaciones más altas van a obtener un premio. ¿Cuántas maneras diferentes hay de obtener los tres ganadores?
- ¿De cuántas maneras diferentes se puede ordenar la palabra Mérida?
No olvides dejar tus dudas, comentarios e inquietudes sobre lo que leíste o si crees que faltó algo.
Comentarios
Publicar un comentario