Las Combinaciones

Si ya leíste mi post sobre las permutaciones, te habrás dado cuenta de que lo que importa en ellas es el orden, es decir, un nuevo orden produce una nueva permutación, aún cundo sean los mismos elementos.

Con las combinaciones el caso es diferente: si son los mismos elementos, no importa el orden en que estén. Es la misma combinación.

Una combinación es cada uno de los pequeños conjuntos que se pueden formar a partir de un conjunto más grande. Sin importar el orden en que ubiques los elementos.

El caso más frecuente en el que nos encontramos ante un problema de combinaciones es cuando vamos a la heladería y queremos un cono de, por ejemplo, tres sabores distintos. Si el vendedor te pone a escoger tus tres sabores de una colección de cinco que tiene, ¿alguna vez te has preguntado cuántos conos diferentes puedes armar? Sabes que el orden en que elijas los sabores no importa. Solo importan los sabores y ya. Cada una de esos conos representa una combinación.

Siguiendo con el ejemplo de los helados, si los sabores son ron con pasas (R), vainilla (V), brownie (B), macadamia (M) y arequipe (A), entonces éstas son todas las combinaciones posibles:

Posiblemente ya te diste cuenta de que no está, por ejemplo, BRV, y la razón es sencilla. EN LAS COMBINACIONES EL ORDEN NO IMPORTA. ESA ES LA MISMA QUE YA ESCRIBÍ EN LA PRIMERA CASILLA, es decir, RVB. Un helado con los sabores ron con pasas, vainilla y brownie es lo mismo que un helado con brownie, ron con pasas y vainilla.

Ahora que ya tienes una idea de qué son las combinaciones, te voy a mostrar la fórmula que debes usar para calcular el número total de éstas. Si n representa el número de elementos del conjunto grande de dónde vas a escoger los elementos para formar tus combinaciones y k, el número de elementos que va a tener cada combinación, entonces el número total de combinaciones, el cual se escribe nCk o a veces C(n,k), es

Si seguimos con el ejemplo de los helados, tenemos lo siguiente:
Nuestra n vale 5, mientras que la k es igual a 3. De modo que el valor que buscamos, lo obtenemos con solo remplazar estas letras por esos números, y es

O sea, son diez combinaciones diferentes. 


Miremos otro ejemplo.

En un grupo de 36 estudiantes, se quiere escoger un comité de 6 de ellos. ¿Cuántos comités distintos se pueden formar?
Solución:
Aquí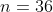  y , entonces





De modo que la cantidad de comités posibles son 7.140.

Espero haya quedado más claro el concepto.
Si tienes alguna duda o inquietud, déjame tu comentario.